20. By using the concept of equation of a line, prove that the three points (3, 0), (– 2, – 2) and (8, 2) are collinear.
20. By using the concept of equation of a line, prove that the three points (3, 0), (– 2, – 2) and (8, 2) are collinear.
Share
To prove that the three points (3, 0), (-2, -2), and (8, 2) are collinear, that means these three points lie on the same line.
Here we need to check whether (8, 2) satisfy the equation made by the point (3, 0) and (-2, -2) or not.
We know that equation of the line passing through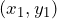 and
and 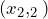 is
is
So, the equation of the line passing through (3, 0) and (-2, -2) is
5y = 2x – 6
2x – 5y – 6 = 0
Since the three points lie on the same line, then point (8, 2) must satisfy the equation 2x – 5y – 6 = 0
putting x = 8 and y = 2 in the above equation
2(8) – 5(2) -6 = 0
16 – 10 – 6 = 0
0 = 0
Which is true
Hence (3, 0), (-2, -2), and (8, 2) are collinear